Visualizing the Trapping Rain Water LeetCode Problem
The “Trapping Rain Water” problem (LeetCode #42) is a classic algorithm challenge: given an array of non-negative integers representing an elevation map, calculate how much water can be trapped between the bars after rain. This is a common question in software engineering interviews and a great way to practice problem-solving with data structures and algorithms.
This visual walkthrough breaks down the calculation using a two-pointer approach, with a left-pass and a right-pass. Lets dive into how this visualization calculates the trapped water with the input height = [0,1,0,2,1,0,1,3,2,1,2,1].
The Core Idea in This Visualization
This method calculates potential water trapped at each position based on the maximum height encountered so far from one direction (either left or right). Assuming the bar height at the beginning of the array is 0 and the end of the array is 1, the calculation will start moving the pointer from the right side of the array.
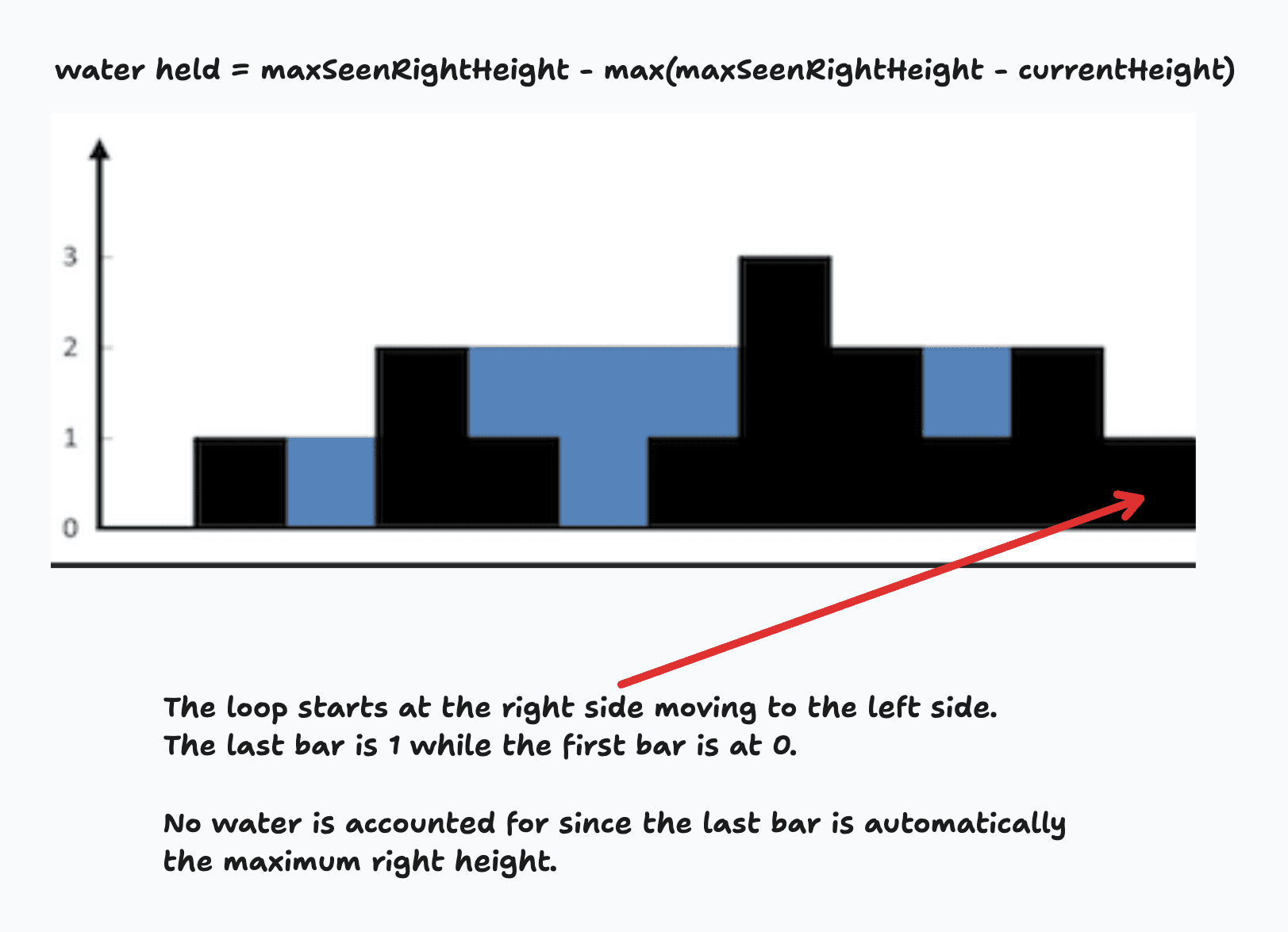
The key formula highlighted is: water held = maximum height - current height
Here, “maximum height” refers to the highest bar seen up to that point during the pass from that specific side.
The Two-Pass Calculation
The image presents the calculation in two distinct columns: “Left” and “Right”.

1. The Right Pass (Working Right-to-Left):
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
The count, or water volume that can be trapped, is initialized to 0. In case there is no water that can be trapped, the result will be 0. To solve a two-pointers problem, we need two pointers for now. The left pointer starts at the beginning of the array at index 0, while the right pointer starts at the end of the array at index height.length - 1. The maxHeightR and maxHeightL are initialized to 0 because the array has non-negative integers.
Lets consider the iterations below*
This pass calculates water based on the maximum height seen from the right (maxHeightR).
- right = 0:
current height = 1. maxHeightR (max seen before this, moving from right) = 1.
Why 1? Remember, before iterating over the array, there was no maxHeightR, and since the shortest bar is no bar, see what I did there, the maxHeightR is initialized to 0. This applies to the maxHeightL too. Water = 1 - 1 = 0. right--
The current height is 1 since height[height.length - 1] = 1.
- right = 1:
current height = 2.maxHeightR= 2. Water =2 - 2 = 0.right-- - right = 2:
current height = 1.maxHeightR= 2. Water =2 - 1 = 1.right-- - right = 3:
current height = 2.maxHeightR= 2. Water =2 - 2 = 0.right-- - right = 4:
current height = 3.maxHeightR= 3. Water =3 - 3 = 0.right-- - right = 5:
current height = 1.maxHeightR= 3. Water =3 - 1 = 2.right-- - right = 6:
current height = 0.maxHeightR= 3. Water =3 - 0 = 3.right--
The total water calculated in this pass is: Units = 6.
2. The Left Pass (Working Left-to-Right):
This pass calculates water based on the maximum height seen from the left (maxHeightL).
- left = 7:
current height = 1.maxHeightL(max seen before this) = 1. Water =1 - 1 = 0.left++ - left = 8:
current height = 0.maxHeightL(max seen before this) = 1. Water =1 - 0 = 1.left++ - left = 9:
current height = 2.maxHeightL(max seen before this) = 2. Water =2 - 2 = 0.left++ - left = 10:
current height = 0.maxHeightL(max seen before this) = 2. Water =2 - 0 = 2.left++ - left = 11:
current height = 1.maxHeightL(max seen before this) = 2. Water =2 - 1 = 1.left++
The total water calculated in this pass is: Units = 3.
Conclusion
This visualization provides a unique way to understand the Trapping Rain Water problem by breaking it down into two separate passes. This two-pointer technique is an efficient way to solve the problem and is a great example of algorithmic thinking in software development.